Hoy quería recordar un poco de teoría de números analítica ya que a veces cuando tenemos un campo, queremos trabajar con los equivalente a sus "enteros" en analogía con $latex \mathbb{Q}$ y sus enteros $latex \mathbb{Z}$.
Entonces comencemos con la definición principal.
Definición: Un campo numérico $latex K$ es una extensión de campos algebraica finita de $latex \mathbb{Q}$
Esto quiere decir que $latex n=[K:\mathbb{Q}]<\infty$ es la dimensión del $latex \mathbb{Q}-$espacio vectorial $latex K$ , a $latex n$ nos referiremos como el grado de esta extensión.
El ejemplo por excelencia es:
$latex \mathbb{Q}(\sqrt{2}) = \lbrace x+y\sqrt{2} : x,y\in \mathbb{Q}\rbrace$
O también pueden considerar $latex \mathbb{Q}(\zeta_n)$ que es al adjuntarle una raíz $latex n-$ésima de $latex 1$ (compleja), $latex \mathbb{R}$ no es un ejemplo de campo.
Ahora, si $latex \alpha\in K$ con $latex K$ de grado $latex n$ como $latex K$ es un $latex \mathbb{Q}-$espacio vectorial entonces existe una dependencia $latex \mathbb{Q}-$lineal entre $latex \lbrace 1,\alpha,...,\alpha^n\rbrace$ (ya que tiene dimensión $latex n$ y hay $latex n+1$ ahí), esto significa que existe un polinomio $latex f(x)\in \mathbb{Q}[x]$ tal que $latex f(\alpha)=0$ , si esto pasa decimos que $latex \alpha$ es un número algebraico y decimos que $latex \alpha$ es un entero algebraico si $latex \alpha$ es raíz de un polinomio mónico en $latex \mathbb[x]$.
Otro ejemplo obligatorio, es que $latex \sqrt{2}\in \mathbb{Q}(\sqrt{2})$ es un entero algebraico ya que es raíz es $latex x^2-2\in\mathbb{Z}[x]$ así como $latex i\in\mathbb{Q}(i)$ ya que es raíz de $latex x^2+1\in \mathbb{Z}[x]$, como es de esperarse $latex a/b\in\mathbb{Q}$ no son enteros (a menos que $latex b\mid a$ ya que no existe un polinomio mónico con coeficientes enteros que los tenga como raíz.
Hasta aquí hemos extendido un poco la definición de lo que es para nosotros un número entero en términos de la existencia de un polinomio mónico con coeficientes enteros.
Definición: El polinomio mínimo de $latex \alpha\in K$ es un $latex f\in\mathbb{Q}[x]$ mónico, tal que $latex f(\alpha)=0$ y $latex f$ es de grado mínimo.
Es un buen ejercicio demostrar que $latex \alpha\in K$ es un entero algebraico si y sólo sí su polinomio mínimo tiene coeficientes enteros.
Si demostramos lo anterior tenemos que con todo esto.
Proposición: Los enteros algebraicos de $latex \mathbb{Q}$ son $latex \mathbb{Z}$
Esto también es fácil ya que si $latex a/b\in\mathbb{Q}$ entonces su mínimo polinomio es $latex x-a/b$ que por el ejercicio anterior sucede que $latex b\in\lbrace -1,1\rbrace$
Definición: Los enteros algebraicos de $latex K$ forman un anillo que lo denotamos como $latex \mathcal{O}_K$ y le llamamos anillo de enteros de $latex K$
El hecho de que $latex \mathcal{O}_K$ forma un anillo no es trivial, o sea, que la suma y producto de enteros algebraicos es un entero algebraico, pero tampoco es tan difícil , traten de visualizarlo con propiedades de sus polinomios moninos, y ver como pueden construir el polinomio monico que corresponde al producto y suma de dos números algebraicos, o también pueden demostrar que si $latex \alpha$ es un entero algebraico entonces $latex \mathbb{Z}[\alpha]$ es finitamente generado como grupo, es decir si $latex z\in \mathbb{Z}[\alpha]$ entonces $latex z=\sum_{i\leq m}z_i n_i$ es decir $latex \mathbb{Z}[\alpha]=\bigoplus_{i\leq m}\alpha^i \mathbb{Z}$.
Como un no-ejemplo tenemos a $latex \mathbb{Z}[\frac{1}{2}]$ está generado por todas las potencias de $latex \frac{1}{2}$ por lo que no es finitamente generado y su polinomio mínimo es $latex x-1/2$
Otros corolarios de esto son que $latex K=\mathbb{Q}\mathcal{O}_K
Normas y trazas de enteros algebraicos
Si $latex L/K$ es una extensión finita de campos numéricos y $latex \alpha\in L$ entonces el mapeo de multiplicación por $latex \alpha$ está dado por:
$latex \mu_\alpha:L\rightarrow L$
$latex x\mapsto \alpha x$
Esto es un mapeo $latex K$-lineal de $latex L$ a $latex L$ es decir un endomorfismo por lo que $latex \mu_\alpha\in End_K(L)$ $latex \forall \alpha\in L$
Como $latex \mu_\alpha \in End_K(L)$ entonces es una matriz y decimos que la norma y traza de $latex \alpha\in L$ están dadas por:
$latex N_{L/K}(\alpha)=det(\mu_\alpha)\in K$
$latex Tr_{L/K}(\alpha)=Tr(\mu_\alpha)\in K$
Tenemos que
$latex N_{L/K}(\alpha\beta)=N_{L/K}(\alpha)N_{L/K}(\beta)$
$latex Tr_{L/K}(\alpha+\beta)=Tr_{L/K}(\alpha)+Tr_{L/K}(\beta)$
por las propiedades de traza y determinantes usuales, por lo que si en particular $latex n=[L:K]$ y $latex a\in K$
$latex N_{L/K}(a\alpha)=a^n N_{L/K}$
$latex Tr_{L/K}(a\alpha)=aTr_{L/K}(\alpha)$
De hecho si $latex a\in K$ entonces $latex \mu_a$ si $latex \mathbb{I}$ es la matriz identidad entonces $latex \mu_a=a\mathbb{I}$.
También tenemos al polinomio característico de $latex \alpha\in L$ definido como:
$latex \chi(x)=det(\mathbb{I}x-\mu_\alpha)\in K[x]$ , donde es fácil ver que su término constante es $latex \pm N_{L/K}(\alpha)$ y el término de $latex x^{n-1}$ es $latex -Tr_{L/K}(\alpha)$ ya que $latex \chi(x)$ es un polinomio mónico de grado $latex n=[L:K]$
Es hora de un Ejemplo
Como lo hemos hecho $latex L=\mathbb{Q}(\sqrt{2})$ y $latex K=\mathbb{Q}$ entonces $latex 2=[L:K]$ por lo que podemos poner una base para el $latex \mathbb{Q}$ espacio vectorial $latex \mathbb{Q}(\sqrt{2})$ , la cual por simplicidad será $latex \lbrace 1,\sqrt{2} \rbrace$, entonces sea $latex \alpha \in \mathbb{Q}(\sqrt{2})$ , ahora calculemos $latex \mu_\alpha$ , tenemos que $latex \alpha = a+b\sqrt{2}$, para calcular la matriz, como vimos anteriormente $latex \mu_\alpha$ es un operador lineal , así que basta con aplicarlo a los elementos de la base para obtener su matriz.
$latex \mu_\alpha(1)=a+b\sqrt{2}$
$latex \mu_\alpha(\sqrt{2})=\sqrt{2}a+2b=2b+a\sqrt{2}$
Por lo que tenemos que:
$latex \mu_\alpha = \begin{pmatrix}a & 2b\\ b&a\end{pmatrix}=M_\alpha$
Ya que si $latex z=s+t\sqrt{2}\in \mathbb{Q}(\sqrt{2})$ entonces
$latex M_\alpha \begin{pmatrix}s\\ t\end{pmatrix}=(as+2bt,bs+at)=as+2bt+(bs+at)\sqrt{2}$
$latex =(a+b\sqrt{2})(s+t\sqrt{2})=\alpha z =\mu_\alpha(z)$
Por lo que $latex N_{\mathbb{Q}(\sqrt{2})/\mathbb{Q}}(\alpha)=a^2-2b^2$ y $latex Tr_{\mathbb{Q}(\sqrt{2})/\mathbb{Q}}(\alpha)=2a$
Y el polinomio característico está dado por:
$latex \chi(x)=det \begin{pmatrix}x-a & -b\\ -2b&x-a\end{pmatrix}=x^2-2ax+a^2-2b^2$
$latex K$-monomorfismos a $latex \overline K=\mathbb{C}$
Para relacionar la traza y norma tenemos que existen $latex n=[L:\mathbb{Q}]$ monomorfismos $latex \sigma_i:L\rightarrow \mathbb{C}$ , ya que si $latex L=K(\alpha)$ con $latex \alpha\in L$ entonces existe $latex f\in K[x]$ polinomio mínimo de $latex \alpha$ y es un resultado sabido que $latex f$ no tiene raices repetidas en $latex \overline{K}=\mathbb{C}$ por lo que tiene $latex n$ raíces diferentes, llamémosles $latex \alpha_i$ y definimos $latex \sigma_i(\alpha)=\alpha_i$, esto se puede demostrar para $latex K(\alpha,\beta)$ y en general por inducción.
Definición: Si $latex L/K$ es una extensión algebraica finita de grado $latex n$ entonces y $latex \alpha\in L$ con $latex \sigma_1, ..., \sigma_n$ los $latex K-$monomorfismos de $latex L$ a $latex \mathbb{C}$ entonces $latex \sigma_1(\alpha), ... , \sigma_n(\alpha)$ son los conjugados de $latex \alpha$
Teorema Sea $latex L/K$ una extension algebraica finita de grado $latex n$ y $latex \sigma_1, ..., \sigma_n$ los $latex K-$monomorfismos de $latex L$ a $latex \mathbb{C}$ que fijan $latex K$ entonces tenemos que para todo $latex \alpha\in L$
$latex N_{L/K}(\alpha)=\prod_{i=1}^{n}\sigma_i{\alpha}$
$latex Tr_{L/K}(\alpha)=\sum_{i=1}^{n}\sigma_i{\alpha}$
Esto se puede demostrar primero notando que si $latex \alpha\in L$ y $latex f\in K[x]$ es su polinomio mínimo, entonces:
$latex f(x)=\chi_{K(\alpha)/K}(x)$ y que por Cayley Hamilton $latex \chi_{K(\alpha)/K}(\mu_\alpha)=0$
Ejemplo
Sea $latex \mathbb{Q}(\sqrt{2})/\mathbb{Q}$ y $latex \alpha=a+b\sqrt{2}\in\mathbb{Q}(\sqrt{2})$ entonces:
$latex \sigma_1(a+b\sqrt{2})=a+b\sqrt{2}$
$latex \sigma_2(a+b\sqrt{2})=a-b\sqrt{2}$
Por lo que:
$latex N_{\mathbb{Q}(\sqrt{2})/\mathbb{Q}}(\alpha)=\sigma_1(a+b\sqrt{2})\sigma_2(a+b\sqrt{2})=a^2-2b^2$
y
$latex Tr_{\mathbb{Q}(\sqrt{2})/\mathbb{Q}}(\alpha)=\sigma_1(\alpha)+\sigma_2(\alpha)$
Que claramente da lo mismo que como lo calculamos anteriormente.
Queda para ustedes que calculen el polinomio característico de este caso, y que también consideren $latex \mathbb{Q}(i,\sqrt{2})$
Corolario $latex N_{K/\mathbb{Q}}(\alpha)=\pm 1$ con $latex \alpha\in \mathcal{O}_K$ $latex \Leftrightarrow$ $latex \alpha$ es invertible
Eduardo Ruiz Duarte (beck)
twitter: @toorandom
Monday, March 30, 2015
Wednesday, March 25, 2015
Homosexuality and evolution, an attempt of an a priori argument to end homophobia
What I am going to say here doesn't have any proof, and maybe is not entirely true, but is something I would like to propose as a conjecture, and I have thought for some time, I don't know the answers a priori, because I am not a professional in other areas in science and sociology, but maybe it could be a good theory and I propose a way to take the proof apriori with a possible argument, maybe you can refute it immediately, but the aim of this is to generate a consistent strong theory to avoid discrimination and homophobia.
In the next words when I say homosexual I will be referring to lesbians or male gays.
Introduction
Lets start, some moments ago I was chatting with a friend, she told me that she has a 'friend' that was a complete retrograde, in the sense that she forbids completely the adoption between homosexuals, or that the best birth control system is god's word in your heart, I do not pretend to offend anybody but if you are going to make an argument trying to forbid or not approve you must have an a priori argument, and not an argument based on a religious belief or a personal point of view, otherwise, you are imposing an idea like a dictator, making you retrograde.
What I am going to say is a possible-scientific reason to stop being an asshole, and maybe could be a good multidisciplinary work between mathematicians, sociologists, philosophers and evolutive biologists.
The next argument relies in the existence of models to measure situations in the nature, that proves that there is an equilibrium in the reproduction of species, interaction between species and natural resources consumption, this equilibrium is well modeled with five theories which I think are the bridges between mathematics, genetics, macro economy, evolutive biology and game theory, these models are described at the end of this post as an appendix, (Lotka-Volterra equations, Malthus model, logistic function, Nash equilibrium and Memetics).
The idea of this is provide a way to prove this:
Conjecture:
Homosexuality is a consequence of evolution.
Development of the conjecture and possible proof:
The models of population growth in terms of natural resources and interaction between species tell us that the convergence of the population when $latex t\rightarrow \infty$ is 0 when the function representing resource consumption is increasing over time, this in common sense is obvious, but more important than obvious, is that it has a mathematical model to prove it, and this models are Malthus equation and Logistic equation.
Another important theory here is Darwinian evolution which occurs with natural selection meaning that the individuals that adapt better to their environment will spread their genes with more frequency because they will be healthier for more time, this better adaptation is done because of a random mutation that makes the individual better than the others in terms of survival circumstances.
Another fact is that there is an excess of population in terms of some resources, (see variable $latex K$ in the logistic equation at the end of this post), there are more humans that the natural resources can support, but this IS NOT because we are lacking of food (this is important to understand), this is because the economic model that prevails (capitalism) bounds this resources in terms of wealth, so there are MORE humans than resources in function of wealth and economy.
So, If you accept the last paragraph, then we can continue, I accept that the last paragraph is a problem that exists, I dont know why but I have an idea that can be wrong or bad, but the veracity of the next paragraph does no depend on the veracity of the original conjeture (is used only to give an idea of why there's an overpopulation)
Conjecture (independent of the original conjecture)
The population increases in function of the advances in medicine
This may sound a little cruel, but we are trying to make science, not ethics.
With the advances of medicine, people that develops a mortal disease young due to a letal gene does not die and reproduces passing his/her lethal gene to the next generations, slowing down evolution, (note that there's no such thing as anti-evolution, evolution always goes up in terms of adaptation).
So, technology in medicine make us overpopulated, note that is easy to show that evolution occurs and there are examples of this, if there were not a treatment of wisdom teeth people would die of impacted teeth or infection at maybe a young age, making the population with wisdom teeth less and less over generations.
In the book Selfish Gene from Richard Dawkins, he mentions that a non ethical way to evolve faster will be to only permit child conception in the biological limit of age in order to permit the death generated by letal genes, and in consequence, more genetically healthy human beings.
Now, lets return to the original idea.
We know now (or at least I hope I could convince you) that there's an overpopulation in terms of some natural resource which at the same time is in function of the economic model, and that the persistence of humans even when "they have to die" makes harder the natural selection.
Now we are in a point where humans in order to win the battle of resources they first most prevail and the Nash Equilibrium (see the end of the post for details) tell us that there's a point over time when the players (humans) with mixed strategies in this battle will take the most efficient decision in terms of the best decisions of the other, which is the equilibrium, if we identify the capabilities of each player (human) we will be sitting in the Lotka-Volterra equations, when we will identify which is the predator and the pray in terms of the economic model.
This Equilibrium I claim is homosexuality, which is the most natural way to solve the overpopulation, and proving that homosexuality is a natural property of the genes, a mutation in the human DNA, just as the mutation of distinguishing frequencies in our eyes and not just amplitude (colors) which was a mutation that prevailed making evolution of our eyes
First questions of this argument with a possible answer
1) Gay people are not new, there are proofs they have been in society from centuries ago and we did not have overpopulation problems.
Possible answer:
Yes, gays have been in the society for centuries,
But what I claim is that overpopulation has been there too since centuries, and as I said before, not because there's not food... is because the overpopulation is in terms of the economic model, people cannot take an apple from a tree without taking it from somebody's territory (in most cases), so he/she has to pay to the wealthiest, this makes Malthus and Logistic model of population vs resources being in function of the capabilities of resource taking, so if this is true (Is a conjecture as I said) it justifies the same argument.
2) Darwinian Evolution confirms that the genes must be spreaded, and homosexuality is not spreaded with a homosexual couple (just in an artificial way which takes you to question 3).
Possible answer:
Darwinian evolution is proved to be at the level of particles (See Dawkins, first chapter of Selfish Gene), particles tend to form stable structures, and this structures tend to form particles that are self replicable, this is the principle of evolution pre-life in the planet, and is proven using the primordial soup experiment which consists in the simulation of the condition of the early earth with methane, hidrogen and amonia in combination with lightening, in a period of time monomers will form, then polymers and then self-replicatation molecules, which are the predecesors of the DNA.
This same behaviour is the basis of Darwinian sociology where the concept of spreading the gene will be a cultural concept for the next generation.
3) Gays can use in vitro methods to procreate children or "rent female" wombs (in the case of male gays)
Possible answer:
For this I need to introduce a concept, Memetics
Memetics (Richard Dawkins work for a treatment):
Theory of mental content based on an analogy with Darwinian evolution, is an approach to evolutionary models of cultural information transfer where the unit transfer is a meme.
Darwinian sociology makes the adaptation, natural selection and gene spreading to be taken in a cultural level, and there it can be introduced the concept of memetics, and consider evolution something more complex in humans than just a biological facts because human are equiped with reasoning and a brain capable of thinking in complex dynamic situations.
Gay people can adopt, procreate artificially or not having children, gays are not capable of reproducing themselves, but when they adopt or procreate they spread the gene that makes them homosexual with a probability of 50%, or in the case of adoption, memetics from Richard Dawkins can be used and they will spread the Meme (See Memetics), which partially answers the previous question and justifies their existence as an evolutionary individual capable of reproducing his/her genes and memes.
Direct consequences of this conjecture
Homosexuality cannot be a disease, or a "condition", in darwinian evolution a mutation that affects the species wont prevail, so homosexuality is a property in human beings making them a naturally evolved organism.
Personal conclusion
Homosexuality is the direct consequence of a future in society when the convergence is of not having men or women, gay or not gay, but having just individuals or human beings, making them the key to find an equilibrium as a specie.
Nash Equilibrium
John Nash proved that in a game, (in this case the battle of resources between humans) with mixed strategies (this means that, if there are different set of specific rules to win a game, you can randomly change strategies to win a game) there's always a point of Nash equilibrium between the parts, this means that , if $latex A$ is compiting with $latex B$ , the Nash equilibrium is the point were $latex A$ has the best decision taking in consideration $latex B$ decisions in the evolution of the game, and the same with $latex B$, $latex B$ has the best decision in consideration of $latex A$
Lotka-Volterra Equations tell us the dynamics of two species, where one of this species is a predator of the other (the prey).
$latex \frac{dx}{dt}=\alpha x -\beta xy$
$latex \frac{dy}{dt}=\delta xy -\gamma y$
This equations tell us that if $latex x$ are the number of preys, and $latex y$ are the number of predators , $latex \frac{dx}{dt}$ and $latex \frac{dy}{dt}$ are the changes in population of each other over time $latex t$, $latex \alpha,\beta,\gamma,\delta$ are values that represent the interaction of the species in terms of statistical analysis via observation.
The solution is a function which will tell you what will happen over time with both species and this equations can be generalized to the interaction of more than two.
Malthus equation
Lotka-Volterra equations can be combined with this equation which tells you how the population of an species grow, and what Malthus proved is that is exponential over time.
$latex P(t)=\hat{P} e^{\lambda t}}$
Where $latex P(t)$ is the population at time $latex t$ and $latex \hat{P}$ is the initial number of individuals, and $latex \lambda}$ is a constant (what we want to convert in a function in this idea) that measures the interaction of this specie with their natural resources (or even with other individuals)
Logistic equation
An improved version of the last one is given when you can measure the MAXIMUM number of individuals $latex K$ that an environment can provide resources in a way that no individual will lack of food or a resource that is natural to their lives.
$latex \frac{dP}{dt}=\lambda P(1-P/K)$
Eduardo Ruíz Duarte (beck)
twitter: @toorandom
In the next words when I say homosexual I will be referring to lesbians or male gays.
Introduction
Lets start, some moments ago I was chatting with a friend, she told me that she has a 'friend' that was a complete retrograde, in the sense that she forbids completely the adoption between homosexuals, or that the best birth control system is god's word in your heart, I do not pretend to offend anybody but if you are going to make an argument trying to forbid or not approve you must have an a priori argument, and not an argument based on a religious belief or a personal point of view, otherwise, you are imposing an idea like a dictator, making you retrograde.
What I am going to say is a possible-scientific reason to stop being an asshole, and maybe could be a good multidisciplinary work between mathematicians, sociologists, philosophers and evolutive biologists.
The next argument relies in the existence of models to measure situations in the nature, that proves that there is an equilibrium in the reproduction of species, interaction between species and natural resources consumption, this equilibrium is well modeled with five theories which I think are the bridges between mathematics, genetics, macro economy, evolutive biology and game theory, these models are described at the end of this post as an appendix, (Lotka-Volterra equations, Malthus model, logistic function, Nash equilibrium and Memetics).
The idea of this is provide a way to prove this:
Conjecture:
Homosexuality is a consequence of evolution.
Development of the conjecture and possible proof:
The models of population growth in terms of natural resources and interaction between species tell us that the convergence of the population when $latex t\rightarrow \infty$ is 0 when the function representing resource consumption is increasing over time, this in common sense is obvious, but more important than obvious, is that it has a mathematical model to prove it, and this models are Malthus equation and Logistic equation.
Another important theory here is Darwinian evolution which occurs with natural selection meaning that the individuals that adapt better to their environment will spread their genes with more frequency because they will be healthier for more time, this better adaptation is done because of a random mutation that makes the individual better than the others in terms of survival circumstances.
Another fact is that there is an excess of population in terms of some resources, (see variable $latex K$ in the logistic equation at the end of this post), there are more humans that the natural resources can support, but this IS NOT because we are lacking of food (this is important to understand), this is because the economic model that prevails (capitalism) bounds this resources in terms of wealth, so there are MORE humans than resources in function of wealth and economy.
So, If you accept the last paragraph, then we can continue, I accept that the last paragraph is a problem that exists, I dont know why but I have an idea that can be wrong or bad, but the veracity of the next paragraph does no depend on the veracity of the original conjeture (is used only to give an idea of why there's an overpopulation)
Conjecture (independent of the original conjecture)
The population increases in function of the advances in medicine
This may sound a little cruel, but we are trying to make science, not ethics.
With the advances of medicine, people that develops a mortal disease young due to a letal gene does not die and reproduces passing his/her lethal gene to the next generations, slowing down evolution, (note that there's no such thing as anti-evolution, evolution always goes up in terms of adaptation).
So, technology in medicine make us overpopulated, note that is easy to show that evolution occurs and there are examples of this, if there were not a treatment of wisdom teeth people would die of impacted teeth or infection at maybe a young age, making the population with wisdom teeth less and less over generations.
In the book Selfish Gene from Richard Dawkins, he mentions that a non ethical way to evolve faster will be to only permit child conception in the biological limit of age in order to permit the death generated by letal genes, and in consequence, more genetically healthy human beings.
Now, lets return to the original idea.
We know now (or at least I hope I could convince you) that there's an overpopulation in terms of some natural resource which at the same time is in function of the economic model, and that the persistence of humans even when "they have to die" makes harder the natural selection.
Now we are in a point where humans in order to win the battle of resources they first most prevail and the Nash Equilibrium (see the end of the post for details) tell us that there's a point over time when the players (humans) with mixed strategies in this battle will take the most efficient decision in terms of the best decisions of the other, which is the equilibrium, if we identify the capabilities of each player (human) we will be sitting in the Lotka-Volterra equations, when we will identify which is the predator and the pray in terms of the economic model.
This Equilibrium I claim is homosexuality, which is the most natural way to solve the overpopulation, and proving that homosexuality is a natural property of the genes, a mutation in the human DNA, just as the mutation of distinguishing frequencies in our eyes and not just amplitude (colors) which was a mutation that prevailed making evolution of our eyes
First questions of this argument with a possible answer
1) Gay people are not new, there are proofs they have been in society from centuries ago and we did not have overpopulation problems.
Possible answer:
Yes, gays have been in the society for centuries,
But what I claim is that overpopulation has been there too since centuries, and as I said before, not because there's not food... is because the overpopulation is in terms of the economic model, people cannot take an apple from a tree without taking it from somebody's territory (in most cases), so he/she has to pay to the wealthiest, this makes Malthus and Logistic model of population vs resources being in function of the capabilities of resource taking, so if this is true (Is a conjecture as I said) it justifies the same argument.
2) Darwinian Evolution confirms that the genes must be spreaded, and homosexuality is not spreaded with a homosexual couple (just in an artificial way which takes you to question 3).
Possible answer:
Darwinian evolution is proved to be at the level of particles (See Dawkins, first chapter of Selfish Gene), particles tend to form stable structures, and this structures tend to form particles that are self replicable, this is the principle of evolution pre-life in the planet, and is proven using the primordial soup experiment which consists in the simulation of the condition of the early earth with methane, hidrogen and amonia in combination with lightening, in a period of time monomers will form, then polymers and then self-replicatation molecules, which are the predecesors of the DNA.
This same behaviour is the basis of Darwinian sociology where the concept of spreading the gene will be a cultural concept for the next generation.
3) Gays can use in vitro methods to procreate children or "rent female" wombs (in the case of male gays)
Possible answer:
For this I need to introduce a concept, Memetics
Memetics (Richard Dawkins work for a treatment):
Theory of mental content based on an analogy with Darwinian evolution, is an approach to evolutionary models of cultural information transfer where the unit transfer is a meme.
Darwinian sociology makes the adaptation, natural selection and gene spreading to be taken in a cultural level, and there it can be introduced the concept of memetics, and consider evolution something more complex in humans than just a biological facts because human are equiped with reasoning and a brain capable of thinking in complex dynamic situations.
Gay people can adopt, procreate artificially or not having children, gays are not capable of reproducing themselves, but when they adopt or procreate they spread the gene that makes them homosexual with a probability of 50%, or in the case of adoption, memetics from Richard Dawkins can be used and they will spread the Meme (See Memetics), which partially answers the previous question and justifies their existence as an evolutionary individual capable of reproducing his/her genes and memes.
Direct consequences of this conjecture
Homosexuality cannot be a disease, or a "condition", in darwinian evolution a mutation that affects the species wont prevail, so homosexuality is a property in human beings making them a naturally evolved organism.
Personal conclusion
Homosexuality is the direct consequence of a future in society when the convergence is of not having men or women, gay or not gay, but having just individuals or human beings, making them the key to find an equilibrium as a specie.
Appendix of used arguments in the previous idea for interaction models for resources modeling in function of population and competition.
Nash Equilibrium
John Nash proved that in a game, (in this case the battle of resources between humans) with mixed strategies (this means that, if there are different set of specific rules to win a game, you can randomly change strategies to win a game) there's always a point of Nash equilibrium between the parts, this means that , if $latex A$ is compiting with $latex B$ , the Nash equilibrium is the point were $latex A$ has the best decision taking in consideration $latex B$ decisions in the evolution of the game, and the same with $latex B$, $latex B$ has the best decision in consideration of $latex A$
Lotka-Volterra Equations tell us the dynamics of two species, where one of this species is a predator of the other (the prey).
$latex \frac{dx}{dt}=\alpha x -\beta xy$
$latex \frac{dy}{dt}=\delta xy -\gamma y$
This equations tell us that if $latex x$ are the number of preys, and $latex y$ are the number of predators , $latex \frac{dx}{dt}$ and $latex \frac{dy}{dt}$ are the changes in population of each other over time $latex t$, $latex \alpha,\beta,\gamma,\delta$ are values that represent the interaction of the species in terms of statistical analysis via observation.
The solution is a function which will tell you what will happen over time with both species and this equations can be generalized to the interaction of more than two.
Malthus equation
Lotka-Volterra equations can be combined with this equation which tells you how the population of an species grow, and what Malthus proved is that is exponential over time.
$latex P(t)=\hat{P} e^{\lambda t}}$
Where $latex P(t)$ is the population at time $latex t$ and $latex \hat{P}$ is the initial number of individuals, and $latex \lambda}$ is a constant (what we want to convert in a function in this idea) that measures the interaction of this specie with their natural resources (or even with other individuals)
Logistic equation
An improved version of the last one is given when you can measure the MAXIMUM number of individuals $latex K$ that an environment can provide resources in a way that no individual will lack of food or a resource that is natural to their lives.
$latex \frac{dP}{dt}=\lambda P(1-P/K)$
Eduardo Ruíz Duarte (beck)
twitter: @toorandom
Monday, March 16, 2015
Intuición en transformada de Fourier discreta y correlaciones entre señales
Me he visto en la necesidad de ocupar un poco de análisis de Fourier, y ahora se está poniendo de moda mucho usar Fourier en teoría de Números como es en uno de los problemas del milenio, que es la conjetura de Goldbach que dice que todo número par mayor que 2 puede expresarse como suma de dos números primos.
Harald Helfgott decidió probar la conjetura de Goldbach débil (todo impar mayor que 5 es suma de 3 primos) hace un par de años usando teorema de Convolución, esto es algo muy de teoría de análisis complejo y real, y yo no me imaginaría que la solución fuera por aquí, el teorema de la convolución generalmente se usa en el contexto de señales y Análisis de Fourier, en otro momento lo expondré aquí, la explicación sencilla de Helfgott y su solución aquí.
Yo no soy experto en Fourier, pero lo he usado para varios proyectos y me interesa mucho, les expongo aquí una manera intuitiva de entender la transformada de Fourier discreta.
La Transformada de Fourier trasforma una función periódica en otra función en el espacio de frecuencia, es decir, busca otra representación de la función en términos de combinaciones lineales de otras funciones, en este caso senos y cosenos, como algunos sabrán, toda función se puede aproximar por senos y cosenos por partes, estos coeficientes de senos y cosenos que arman la función original son la información de la transformada de Fourier de una función $latex f$.
$latex \hat{f}(\psi)=\int_{-\infty}^{+\infty}f(t)e^{-2\pi it\psi}dt$
donde su inversa está dada por
$latex f(t)=\int_{-\infty}^{+\infty}\hat{f}(\psi)e^{2\pi i\psi t}d\psi$
Harald Helfgott decidió probar la conjetura de Goldbach débil (todo impar mayor que 5 es suma de 3 primos) hace un par de años usando teorema de Convolución, esto es algo muy de teoría de análisis complejo y real, y yo no me imaginaría que la solución fuera por aquí, el teorema de la convolución generalmente se usa en el contexto de señales y Análisis de Fourier, en otro momento lo expondré aquí, la explicación sencilla de Helfgott y su solución aquí.
Yo no soy experto en Fourier, pero lo he usado para varios proyectos y me interesa mucho, les expongo aquí una manera intuitiva de entender la transformada de Fourier discreta.
La Transformada de Fourier trasforma una función periódica en otra función en el espacio de frecuencia, es decir, busca otra representación de la función en términos de combinaciones lineales de otras funciones, en este caso senos y cosenos, como algunos sabrán, toda función se puede aproximar por senos y cosenos por partes, estos coeficientes de senos y cosenos que arman la función original son la información de la transformada de Fourier de una función $latex f$.
$latex \hat{f}(\psi)=\int_{-\infty}^{+\infty}f(t)e^{-2\pi it\psi}dt$
donde su inversa está dada por
$latex f(t)=\int_{-\infty}^{+\infty}\hat{f}(\psi)e^{2\pi i\psi t}d\psi$
Donde $latex t$ es el tiempo y $latex f(t)$ es el valor de la señal en el tiempo $latex t$, $latex e^{2\pi i t}=cos(2\pi t)+isen(2\pi t)$ y $latex \psi$ es el valor de frecuencia.
La teoría aquí es muy bonita, pero también muy complicada, así que nos adentraremos en la parte discreta
Transformada de Fourier discreta.
La transformada de Fourier discreta (TFD) es un funcional (una función de funciones) que toma como argumento una función $latex f$ que es una señal en el tiempo y te regresa otra función $latex \hat{f}$ que contiene la información de la frecuencia en la señal original.
Para términos prácticos, una señal será sólo una sucesión de números, por ejemplo:
$latex \tilde{f}=\lbrace 1.9, -3.1, 12.3,4.8,22.9,-13.2, 11.8,4.8,-0.3 \rbrace$
Dónde $latex \tilde{f}(n)$ es el valor $latex n-$ésimo comenzando por el $latex 0$, $latex \tilde{f}(0)=1.9$
Le pongo tilde porque queremos trabajar con otra versión de esta señal que ahora explico.
Señales de promedio cero
Queremos comparar señales, para ello necesitamos trabajar con las señales "normalizadas" , en el sentido que si vamos a correlacionar $latex f$ con $latex g$ , una correlación "0" nos indique que son totalmente diferentes, para esto, sólo basta con trabajar con las señales "centradas" en su promedio y basta con restar a cada coeficiente el promedio de la señal en el intervalo de tiempo, si repitiéramos esto en la señal verían que el promedio de la señal ya sería 0 y no habría nada que restar, por eso le llamo "normalización" , en el caso del ejemplo, vemos que el promedio es $latex 4.6$ por lo que la nueva señal quedaría.
$latex f=\lbrace -2.7,-7.7,7.7,.2,18.3,-17.8,7.2,.2,-4.9 \rbrace$
La cual tiene promedio 0.
Correlación entre dos señales
Ahora, ¿cómo comparo dos señales normalizadas $latex f$ y $latex g$?
La manera más usual para señales discretas de tamaño $latex N$:
$latex \displaystyle \sum_{i=0}^N {f(i)g(i)}$
Si se fijan, gracias a la normalización tenemos las señales centradas en su promedio, por lo que si esta suma da 0 nos indicaría que no se parecen nada, ya que si $latex f(i)g(i)\geq 0$ es porque ambos valores tienen el mismo signo $latex f(i)g(i)\leq 0$ nos indicaría que difieren en signo y son "muy diferentes" , las sumas se van a ir acumulando positivamente si no hay estos cambios de signo, por lo que indica que entre más grande sea el número de la suma, más grande es la correlación siendo el máximo de correlación la suma de cuadrados de cada señal, si es un número muy grande negativo indicará que están inversamente correlacionadas (no se cancelan con los positivos) , y si es 0 , es porque las correlaciones siempre se "matan" entre negativas y positivas (no hay correlación).
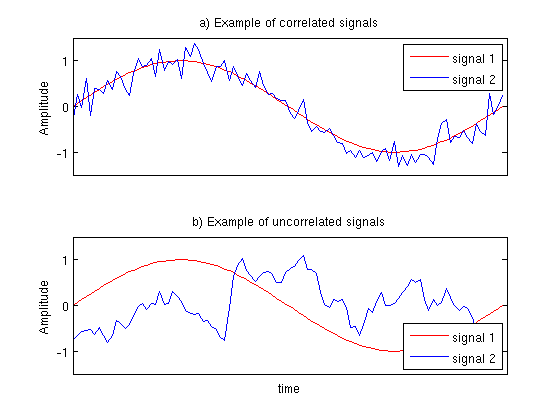
Aquí dejo como se ven dos señales correlacionadas y no correlacionadas.
Para que esta medida tenga sentido, recuerden que tienen que normalizar ambas señales.
Ahora, entonces, si recuerdan, la transformada de Fourier, se multiplica la función por una exponencial compleja, es decir, están correlacionando la función con una exponencial compleja que al final son senos y cosenos, es decir... están comparando la función con senos y cosenos, y viendo qué tanto se parecen en cierto tiempo $latex t$.
La transformada para tiempo discreto $latex n$ de Fourier para una señal $latex f$ de $latex N$ valores en el tiempo se define como:
$latex F(k):=\displaystyle \sum_{n=0}^{N-1} {f(n)e^{{-2\pi i kn}/N}}$ donde $latex k\in \lbrace 0,...,N-1\rbrace$
Para cada $latex k$ obtenemos un coeficiente de Fourier, hasta ahora... creo que vamos bien, no es difícil en términos prácticos, pero ... qué es correlacionar con la exponencial compleja esa? , se ve feo y raro, pero no, recuerden que.
$latex e^{-i\theta} = cos(\theta)-isen(\theta)$
Entonces realmente tenemos que:
$latex F(k):=\displaystyle \sum_{n=0}^{N-1} {f(n)(cos({2\pi kn}/N) - i sen({2\pi kn}/N))$
$latex F(k):=\displaystyle \sum_{n=0}^{N-1} {f(n)cos({2\pi kn}/N)}-i\displaystyle \sum_{n=0}^{N-1} {f(n)sen({2\pi kn}/N)}$
Tenemos que para $latex k$ hay una función diferente.
El juego de signos es por las propiedades de paridad del seno y coseno.
Entonces lo que tenemos aquí es que la transformada de fourier realmente guarda la información en senos y cosenos que es lo que dijimos al principio (para eso se usa la exponencial) , es decir correlaciones con ambos tipos de sinusoides, y el usar la parte compleja, tiene un significado tan simple, como el hecho de hacer "linealmente independientes" a las correlaciones, ya que al final lo que nos interesará será el número real que multiplica a la parte imaginario, y no per sé la $latex i$ de análisis complejo (al menos no en este caso).
¿De qué nos sirve?
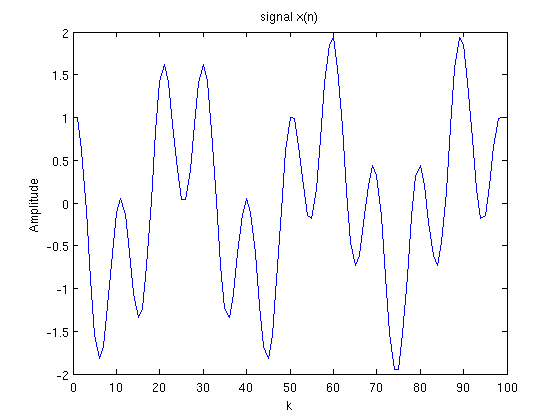
Veamos un ejemplo, supongamos que tenemos la siguiente señal $latex x(n)$ con 100 sampleos de tiempo, es decir $latex N=100$
En este caso los coeficientes para cada seno y coseno definido por $latex k$ los denotaremos como $latex X(k)$, es decir.
$latex X(k)=\displaystyle \sum_{n=0}^{N-1} {x(n)cos({2\pi kn}/N)}-i\displaystyle \sum_{n=0}^{N-1} {x(n)sen({2\pi kn}/N)}$
Para $latex k=0$ tenemos que $latex \displaystyle \sum_{i=0}^{N-1}x(n)$
Es decir solo es la suma de los valores de la señal ($latex sen(0)=0$ , $latex cos(0)=1$)
Por lo que $latex X(0)\cong 0$ ya que la señal está normalizada y tiene promedio 0.
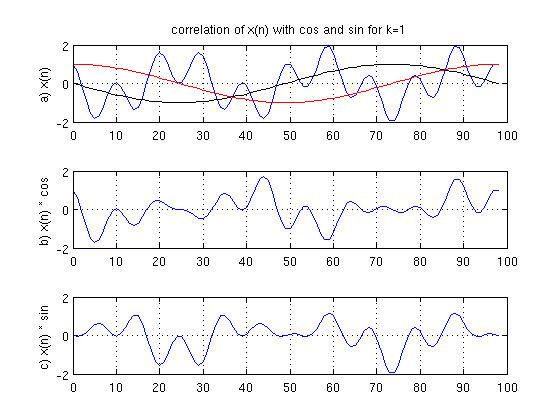
Para $latex k=1$ tenemos la siguiente información de cada sumando de la serie la transformada de fourier.
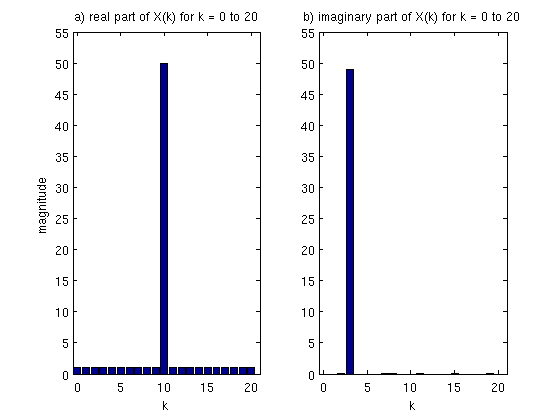
Como pueden ver en la gráfica b) y c) que la $latex X(1)=1+0i$ , es decir, no se parece nada la señal $latex x(n)$ en azul a la negra y roja tanto en seno como en coseno, pueden ver en b) , sin ser muy rigurosos en la siguiente oración: "la mitad de la señal está arriba del 0, y la otra mitad abajo" por lo que la correlación dará 0, lo mismo con c), también se cancela al sumarse sus valores. es decir, no se parecen (recuerden que b, respectivamente c) es la parte (real respectivamente compleja) de $latex X(1)$.
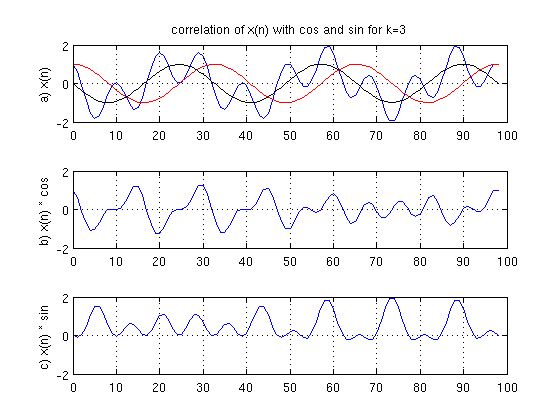
Ahora, veamos que pasa en $latex k=3$
Aquí vemos en $latex k=3$ que el seno con la señal en c) tiene gran parte positiva, y poco negativo...
por lo que la correlación nos indicará que es grande (no se cancela con negativos en la función original) y si ven en a) , pueden ver que el seno en negro en esa $latex k$ "asemeja" a la función $latex x(n)$ mientras que el coseno realmente no se parece en nada, nunca coincide con $latex x(n)$... y de hecho $latex X(3)=0+49i$.
Realmente lo que estamos buscando aquí en la transformada de Fourier, es cuando una senoidal se parece a la función original... y qué creen? , ya la encontramos,
La gráfica de esta transformada de fourier se ve así para $latex k=1...20$
Como pueden ver, la transformada de Fourier, nos dice que $latex X(10)$ en el coseno se parece mucho a la función $latex x(n)$ y en $latex k=3$ tenemos que $latex X(3)$ en la parte imaginaria el seno se parece mucho a la función original, es decir hay correlación alta por ejemplo en el coseno con $latex cos(\pi t/5)$.
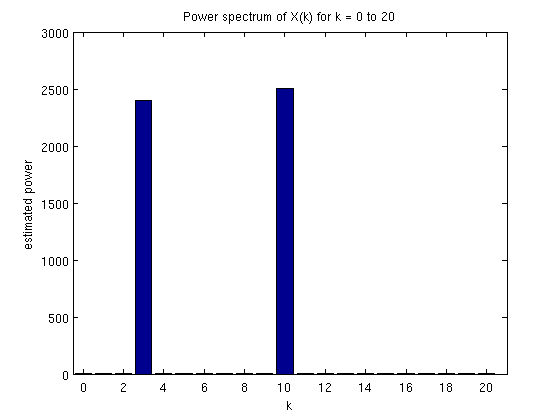
Pero bueno Si quiere ver todo de golpe, sin importarles si es seno y coseno (al final ambas funciones son la misma solamente recorridas) , pueden calcular su densidad espectral para cada valor $latex k$ la cual les dirá si hay sinusoides presentes en la señal la cual se define como
$latex DS_{k}(x)=\mathfrak{R}(X(k))^2 + \mathfrak{I}(X(k))^2$
Que es la suma de los cuadrados de la parte real e imaginaria de la transformada de Fourier para cada $latex k$
Por lo que en este ejemplo, la gráfica de la densidad espectral que ya carece de parte imaginaria, junta toda la información (aunque se pierde de qué tipo de sinodal viene, pero esto es fácil deducirlo)
Aquí pueden ver perfectamente que en $latex k=3$ y en $latex k=10$ existen sinusoides interesantes muy correlacionadas con la señal,
Mucho se habla de Frecuencia, para esto, lo más popular es usar Hz , es decir "cosas que suceden en un segundo" , y para transformar la $latex k$ en Hz , basta decidir "cada cuanto sucede un suceso" a este número llamale $latex r$ , uso $latex r$ porque es de "sampling rate" , y tenemos que en Hz, la frecuencia es $latex \xi=kr/N$ donde $latex N$ es el número de samples, o el número de valores en tu tiempo discreto, entonces ya pueden sustituir la $latex k$ por la frecuencia $latex \xi$.
Espero les haya servido como a mi, las imágenes las saqué de este sitio
Aquí les dejo del mismo sitio los valores de la señal $latex x[n]$ en el ejemplo.
1.000000, 0.616019, -0.074742, -0.867709, -1.513756, -1.814072, -1.695685, -1.238285, -0.641981, -0.148568, 0.052986, -0.099981, -0.519991, -1.004504, -1.316210, -1.277204, -0.840320, -0.109751, 0.697148, 1.332076, 1.610114, 1.479484, 1.039674, 0.500934, 0.100986, 0.011428, 0.270337, 0.767317, 1.286847, 1.593006, 1.522570, 1.050172, 0.300089, -0.500000, -1.105360, -1.347092, -1.195502, -0.769329, -0.287350, 0.018736, -0.003863, -0.368315, -0.942240, -1.498921, -1.805718, -1.715243, -1.223769, -0.474092, 0.298324, 0.855015, 1.045127, 0.861789, 0.442361, 0.012549, -0.203743, -0.073667, 0.391081, 1.037403, 1.629420, 1.939760, 1.838000, 1.341801, 0.610829, -0.114220, -0.603767, -0.726857, -0.500000, -0.078413, 0.306847, 0.441288, 0.212848, -0.342305, -1.051947, -1.673286, -1.986306, -1.878657, -1.389067, -0.692377, -0.032016, 0.373796, 0.415623, 0.133682, -0.299863, -0.650208, -0.713739, -0.399757, 0.231814, 0.991509, 1.632070, 1.942987, 1.831075, 1.355754, 0.705338, 0.123579, -0.184921, -0.133598, 0.213573, 0.668583, 0.994522, 1.000000
Eduardo Ruíz Duarte (beck)
twitter: @toorandom
Subscribe to:
Posts (Atom)